Any circuit is divided into two parts : 

1. Combinational Circuits

2. Sequential Circuits 

Combinational Circuits : 

Combinational circuits are fundamental digital logic building blocks where the outputs are purely determined by the current input values at any given moment. Unlike their sequential counterparts, these circuits have no memory of past events - they respond instantaneously to input changes, much like a light switch that immediately illuminates a room when flipped.

Think of combinational circuits as digital truth machines - they evaluate logical relationships and produce consistent, predictable results. Just as a calculator always gives you the same answer for 2+3, a combinational circuit will always produce identical outputs for identical inputs, regardless of when or how many times you apply those inputs.

Fundamental Characteristics:

• Memoryless Operation: Outputs respond instantaneously to input changes without retaining any information about previous states. The circuit has complete "amnesia" about its history.

• Unidirectional Information Flow: Data travels in a single direction from inputs to outputs, with no feedback paths that could create loops or oscillations. This ensures stable, predictable behavior.

• Asynchronous Response: Unlike sequential circuits that wait for clock edges, combinational circuits operate continuously and respond immediately to input transitions, limited only by the physical propagation delays of the gates.

• Deterministic Behavior: The circuit acts as a pure function - the same input combination will always produce the same output combination, making analysis and verification straightforward.

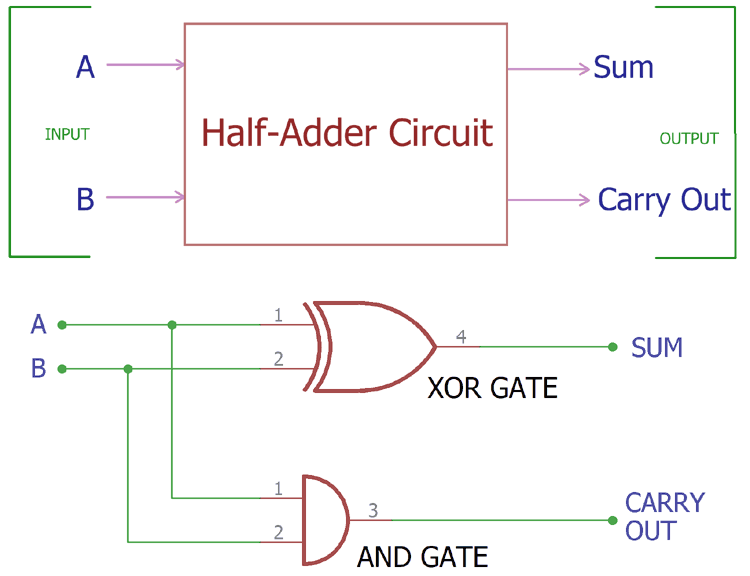
Half Adder

Real-Life Context: The Foundation of Digital Arithmetic

Imagine you're designing a simple digital thermometer that needs to add temperature readings from two sensors. The half adder is like having a basic adding machine that can handle the simplest case - adding two single-digit binary numbers.

Real-World Example: Digital Voting System In electronic voting machines, when counting "Yes" and "No" votes from two districts, a half adder circuit can determine if there's an overall majority and whether there's a tie that needs to be escalated to the next level.

Theory

A half adder is the most basic arithmetic building block in digital systems. It performs addition of two single binary digits, producing a sum and a carry output. It's called "half" because it handles only two inputs without considering any carry from previous operations.

Truth Table

where S = Sum, C = Carry

Real-world interpretation:

• A=0, B=0: No votes from either district → No majority, no escalation

• A=0, B=1: One vote → Majority decided, no escalation needed

• A=1, B=0: One vote → Majority decided, no escalation needed

• A=1, B=1: Both districts vote → Tie situation, escalate to higher authority

Boolean Expressions

• Sum (S) = A ⊕ B (XOR operation)

• Carry (C) = A · B (AND operation)

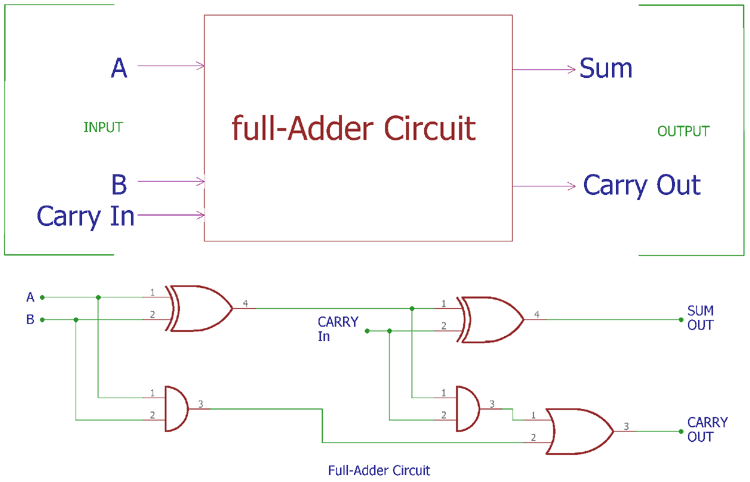
Full Adder

Theory

A full adder is a combinational circuit that adds three binary inputs: two significant bits (A and B) and a carry input (Cin) from a previous stage. It produces a Sum (S) and Carry output (Cout).

Truth Table

Boolean Expressions

• Sum (S) = A ⊕ B ⊕ Cin

• Carry (Cout) = AB + Cin(A ⊕ B) = AB + ACin + BCin

It can be implemented in below ways : 

Implementation Methods

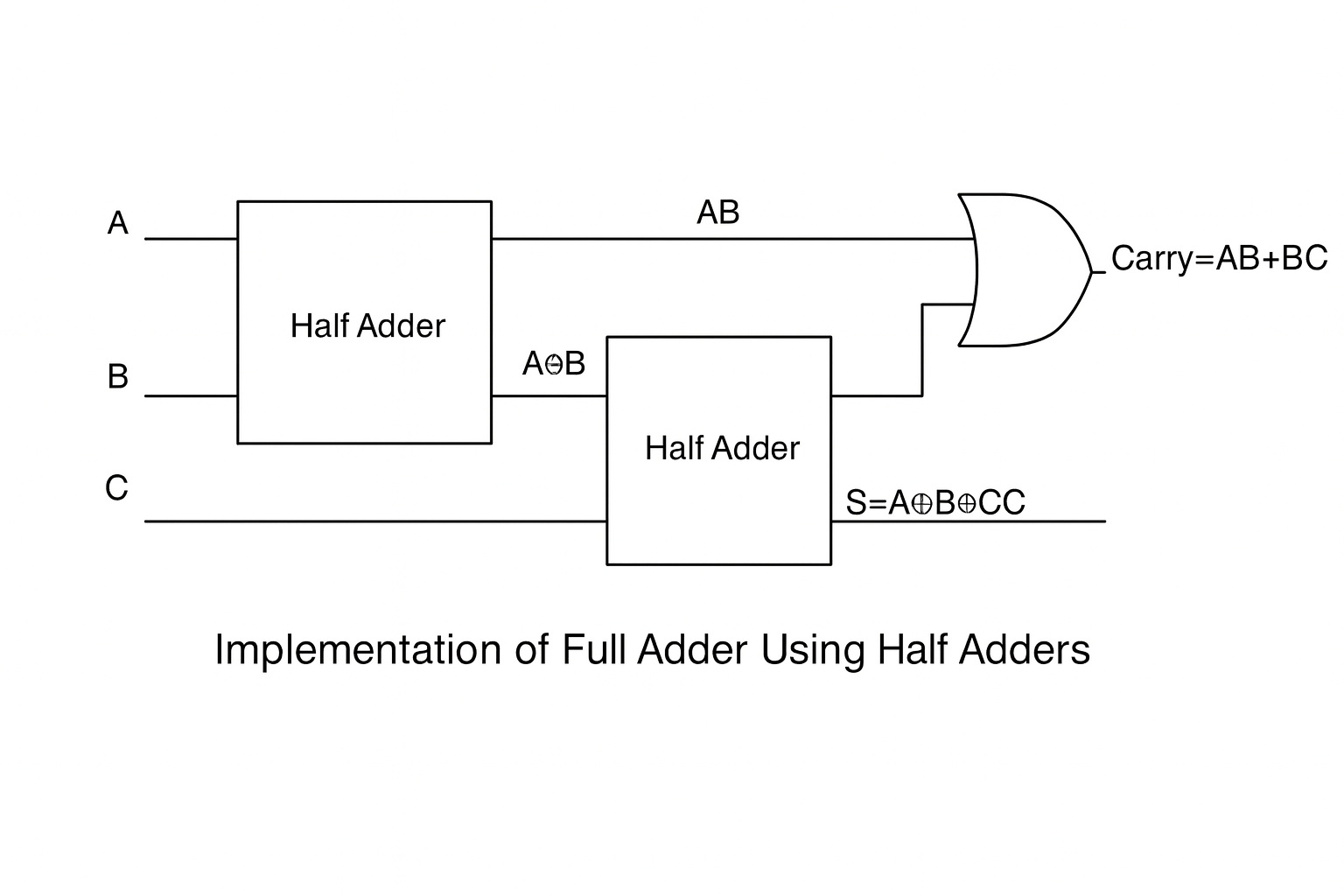
1. Using two half adders and one OR gate

2. Direct gate implementation using XOR, AND, and OR gates

3. Using NAND gates only (9 NAND gates required)

Full Adder using Half Adder : 

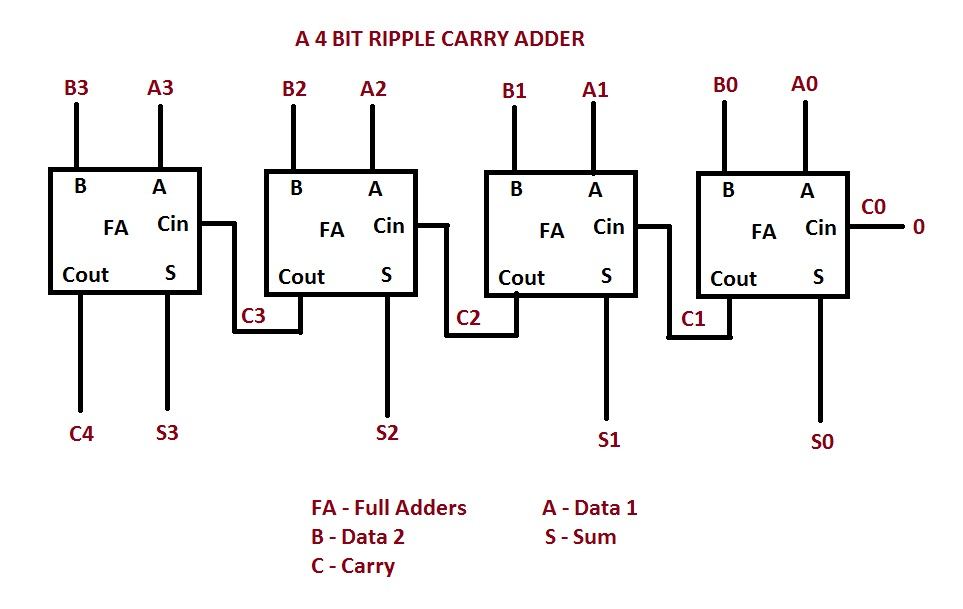
Ripple Carry Adder

What is a Ripple Carry Adder?

A ripple carry adder is a multi-bit adder circuit constructed by cascading multiple full adders. The carry output from each stage "ripples" to the carry input of the next higher-order stage, creating a chain reaction of carry propagation.

Subtractors : 

Half Subtractors : 

A half subtractor performs subtraction of two binary digits (A - B), producing a difference and borrow output.

Truth Table

Banking Example Interpretation:

• A=1, B=0: Have money (1), spending nothing (0) → Keep money (1), no debt (0)

• A=0, B=1: No money (0), trying to spend (1) → Overdraft (1), need to borrow (1)

BLock Diagram : 

Boolean Expressions

• Difference (D) = A ⊕ B

• Borrow (Bo) = A̅ · B

Real-Life Context: Digital Financial Systems

Subtraction is everywhere in digital systems, but it's often hidden. Every time you make a purchase online, withdrawal from an ATM, or transfer money, subtraction circuits are working behind the scenes.

Real-World Example: ATM Transaction Processing When you withdraw $100 from your account:

1. Current balance: $1,247

2. Withdrawal amount: $100

3. ATM fee: $3

4. The system performs: $1,247 - $100 - $3 = $1,144

This requires multiple subtraction operations, each potentially generating "borrows" that propagate through the calculation, just like in binary subtraction circuits.

Full Subtractor : 

Truth Table

Boolean Expressions

• Difference (D) = A ⊕ B ⊕ Bin

• Borrow (Bout) = A̅B + Bin(A ⊕ B)̅

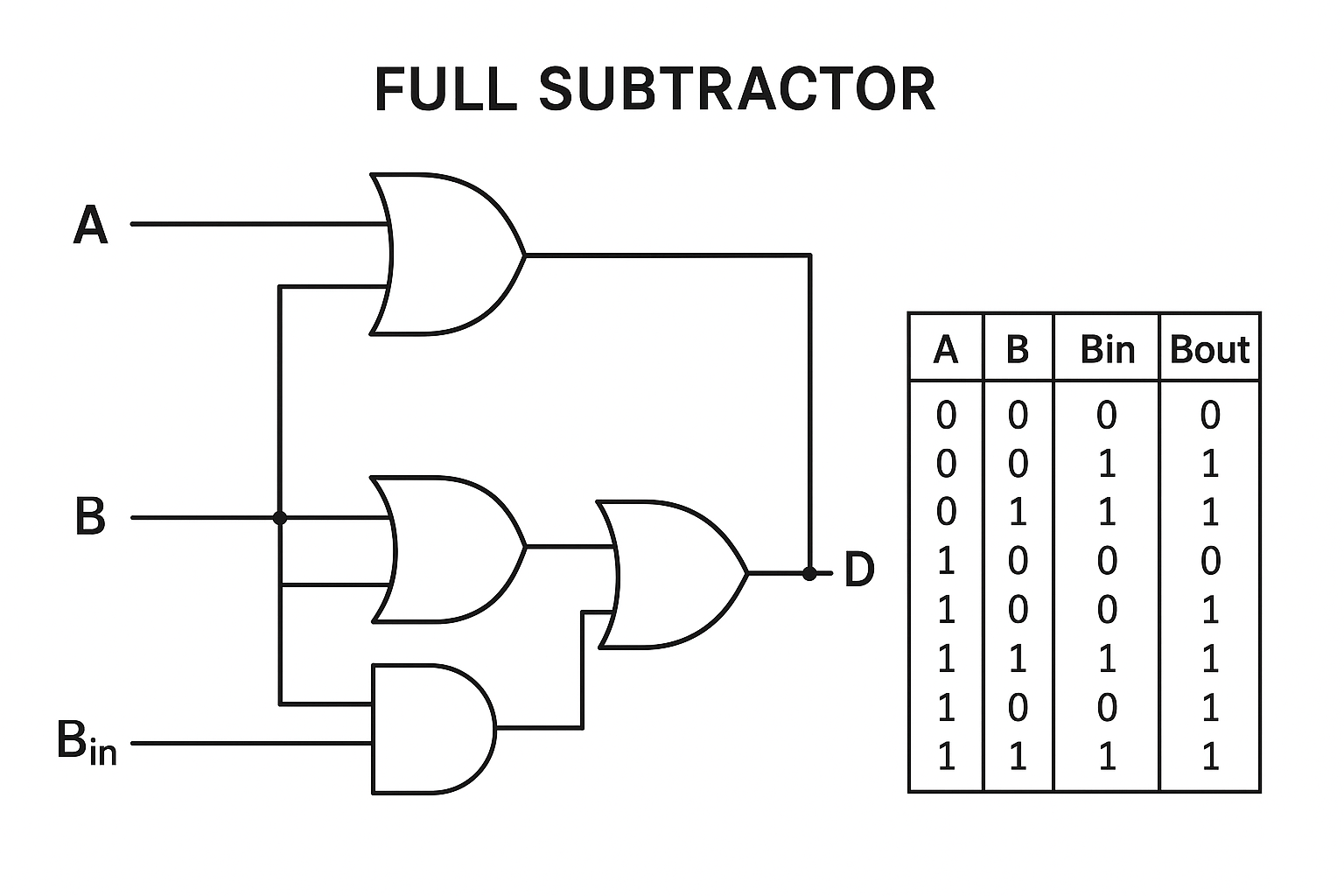
A full-subtractor is a combinational circuit that has three inputs A, B, bin and two outputs d and b. Where, A is the minuend, B is subtrahend, b_in is borrow produced by the previous stage, d is the difference output and b is the borrow output.

As we know that the half-subtractor can only be used for subtraction of LSB (least significant bit) of binary numbers. If there is any borrow during the subtraction of the LSBs of two binary numbers, then it will affect the subtraction of next stages. Therefore, the subtraction with borrow are performed by a full subtractor.

Applications of Full Subtractor

The following are some important applications of full subtractor −

• Full subtractors are extensively used to perform arithmetical operations like subtraction in electronic calculators and many other digital devices.

• Full subtractors are used in ALU (Arithmetic Logic Unit) in computers CPUs.

• Full subtractors are used in different microcontrollers for arithmetic subtraction.

• Full subtractors are also used in processors to compute addresses, tables, etc.