The binary number system uses only two digits, 0 and 1, to represent all data in computing and digital electronics. Understanding unsigned and signed numbers is important for efficient data handling and accurate computations in these fields.

• The binary system forms the foundation of all digital systems, enabling devices to process and store data.

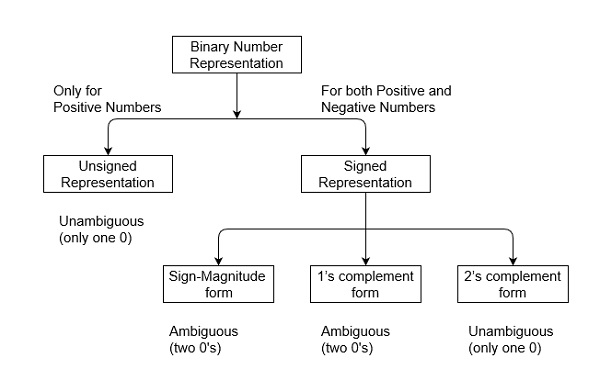
• Unsigned numbers represent only positive values while signed numbers handle both positive and negative values using methods like two’s complement.

• Mastering these concepts is essential for programming, error-free calculations and optimizing system performance.

• Its real-world applications include computer arithmetic, embedded systems and digital signal processing

Unsigned Numbers:

Unsigned numbers don’t have any sign, these can contain only magnitude of the number. So, representation of unsigned binary numbers are all positive numbers only. For example, representation of positive decimal numbers are positive by default. We always assume that there is a positive sign symbol in front of every number.

Representation of Unsigned Binary Numbers:

Since there is no sign bit in this unsigned binary number, so N bit binary number represent its magnitude only. Zero (0) is also unsigned number. This representation has only one zero (0), which is always positive. Every number in unsigned number representation has only one unique binary equivalent form, so this is unambiguous representation technique. The range of unsigned binary number is from  0 to (2ⁿ-1).

Example-1: Represent decimal number 92 in unsigned binary number.

Simply convert it into Binary number, it contains only magnitude of the given number.
= (92)₁₀

= (1x2⁶+0x2⁵+1x2⁴+1x2³+1x2²+0x2¹+0x2⁰)₁₀

= (1011100)₂

It’s 7 bit binary magnitude of the decimal number 92.

Example-2: Find range of 5 bit unsigned binary numbers. Also, find minimum and maximum value in this range.

Since, range of unsigned binary number is from  0 to (2ⁿ-1). Therefore, range of 5 bit unsigned binary number is from  0 to (2⁵-1) which is equal from minimum value 0 (i.e., 00000) to maximum value 31 (i.e., 11111).

2. Signed Numbers:

Signed numbers contain sign flag, this representation distinguish positive and negative numbers. This technique contains both sign bit and magnitude of a number. For example, in representation of negative decimal numbers, we need to put negative symbol in front of given decimal number.

Representation of Signed Binary Numbers:

There are three types of representations for signed binary numbers. Because of extra signed bit, binary number zero has two representation, either positive (0) or negative (1), so ambiguous representation. But 2’s complementation representation is unambiguous representation because of there is no double representation of number 0. These are: Sign-Magnitude form, 1’s complement form, and 2’s complement form which are explained as following below.

2.(a) Sign-Magnitude form:

For n bit binary number, 1 bit is reserved for sign symbol. If the value of sign bit is 0, then the given number will be positive, else if the value of sign bit is 1, then the given number will be negative. Remaining (n-1) bits represent magnitude of the number. Since magnitude of number zero (0) is always 0, so there can be two representation of number zero (0), positive (+0) and negative (-0), which depends on value of sign bit. Hence these representations are ambiguous generally because of two representation of number zero (0). Generally sign bit is a most significant bit (MSB) of representation. The range of Sign-Magnitude form is from  (2^(n-1)-1)  to (2^(n-1)-1).

For example, range of 6 bit Sign-Magnitude form binary number is from  (2⁵-1)  to (2⁵-1) which is equal from minimum value -31 (i.e., 1 11111) to maximum value +31 (i.e., 0 11111). And zero (0) has two representation, -0 (i.e., 1 00000)  and +0 (i.e., 0 00000).

2.(b) 1’s complement form:

Since, 1’s complement of a number is obtained by inverting each bit of given number. So, we represent positive numbers in binary form and negative numbers in 1’s complement form. There is extra bit for sign representation. If value of sign bit is 0, then number is positive and you can directly represent it in simple binary form, but if value of sign bit 1, then number is negative and you have to take 1’s complement of given binary number. You can get negative number by 1’s complement of a positive number and positive number by using 1’s complement of a negative number. Therefore, in this representation, zero (0) can have two representation, that’s why 1’s complement form is also ambiguous form. The range of 1’s complement form is from  (2^(n-1)-1)  to (2^(n-1)-1) .

For example, range of 6 bit 1’s complement form binary number is from  (2⁵-1)  to (2⁵-1) which is equal from minimum value -31 (i.e., 1 00000) to maximum value +31 (i.e., 0 11111). And zero (0) has two representation, -0 (i.e., 1 11111)  and +0 (i.e., 0 00000).

2.(c) 2’s complement form:

Since, 2’s complement of a number is obtained by inverting each bit of given number plus 1 to least significant bit (LSB). So, we represent positive numbers in binary form and negative numbers in 2’s complement form. There is extra bit for sign representation. If value of sign bit is 0, then number is positive and you can directly represent it in simple binary form, but if value of sign bit 1, then number is negative and you have to take 2’s complement of given binary number. You can get negative number by 2’s complement of a positive number and positive number by directly using simple binary representation. If value of most significant bit (MSB) is 1, then take 2’s complement from, else not. Therefore, in this representation, zero (0) has only one (unique) representation which is always positive. The range of 2’s complement form is from  (2^(n-1))  to (2^(n-1)-1).

For example, range of 6 bit 2’s complement form binary number is from  (2⁵)  to (2⁵-1) which is equal from minimum value -32 (i.e., 1 00000) to maximum value +31 (i.e., 0 11111). And zero (0) has two representation, -0 (i.e., 1 11111)  and +0 (i.e., 0 00000).

BCD :

Binary Coded Decimal (BCD) is a binary encoding system in which each decimal digit is represented by a fixed number of binary bits, typically four. Instead of converting the entire decimal number into a binary number, BCD represents each decimal digit separately as its binary equivalent.

• BCD powers digital systems like clocks and calculators, making decimal displays possible.

• It’s the go-to choice for systems with human interaction, like digital displays and data entry tools.

• BCD makes arithmetic easier by treating each decimal digit separately.

• Embedded systems rely on BCD for fast and efficient decimal operations.

Working of Binary Coded Decimal

In BCD, each decimal digit (0-9) is converted into its 4-bit binary equivalent. For example:

• Decimal 0 is represented as 0000 in BCD.

• Decimal 1 is represented as 0001 in BCD.

• Decimal 2 is represented as 0010 in BCD and so on.

For instance, the decimal number 57 would be represented in BCD as two separate 4-bit binary numbers:

• Decimal 5 becomes 0101

• Decimal 7 becomes 0111

So, 57 in BCD is represented as 0101 0111.

Excess-3 code is a non-weighted BCD (Binary Coded Decimal) code. It is called excess-3 code because it is obtained by adding 0011 (3) to the 8421 BCD code. Also called XS-3, the excess 3 code is a BCD code that represents each decimal digit as a 4-bit binary code.

The excess-3 binary code is a sequential code, so we can use it to perform arithmetic operations. Also, it is a self-complementing code, therefore the subtraction operation by the complement method is simpler than that in the 8421 BCD code.

However, in the excess-3 code, there are six invalid codes, they are 0000, 0001, 0010, 1110, and 1111.

How to Obtain Excess-3 Code?

We can obtain the excess-3 code by adding 0011 (3) to the natural 8421 BCD code. It is explained here −

Decimal digit = 0
8421 BCD code = 0000
Excess-3 code = 0000 + 0011 = 0011

Decimal digit = 1
8421 BCD code = 0001
Excess-3 code = 0001 + 0011 = 0100

Importance of Excess-3 Code in Digital Electronics

Excess-3 code is one of the widely used binary codes in early digital systems. Here are some of the key reasons why excess-3 code was used in the field of digital electronics −

• It provides a simplified way of converting a decimal number into binary code.

• It has self-complementing property that makes it suitable for error detection and correction applications.

• It is sequential code, hence it can be used to perform arithmetic operations in digital systems.

• Excess-3 code is highly compatible with decimal IO devices. Thus, it provides a convenient interface between digital systems and other devices.

Advantages of Excess-3 Code

Although, the excess-3 code is less common in modern digital systems. But it has the following key benefits over other binary coding schemes −

• Excess-3 code provides an easy method of representing decimal numbers in binary form.

• Excess-3 code provides an easier way of performing addition and subtraction operations without using any complex conversion methods.

• Excess-3 code is quite easy to convert to and from decimal numbers.

• Excess-3 code being a binary-coded decimal is highly compatible with a wide range of decimal devices.

Disadvantages of Excess-3 Code

Excess-3 code has several advantages, but it also has certain disadvantages as well thats why it is less commonly used in modern digital systems. The following are some key disadvantages of excess-3 code −

• Excess-3 code is an inefficient binary representation of decimal numbers as compared to pure binary. This is because it requires more bits to represent a decimal digit.

• Excess-3 code requires additional arithmetic circuit to add 3 to the standard binary code.

• Excess-3 code has limited compatibility with pure binary systems.

Applications of Excess-3 Code

Excess-3 code was widely used in early digital systems and digital computers. The key areas of excess-3 code applications are listed below −

• Excess-3 code was used in early digital computers.

• Excess-3 code is also used in decimal data processing through digital systems.

• Excess-3 code is also used in digital devices likes printers, card readers, etc. where decimal data is employed.

• The self-complementing property of excess-3 code makes it suitable to use in error detection and correction applications.

• Excess-3 code is also communication and data transmission applications.

Hamming code is an error-correcting code used to ensure data accuracy during transmission or storage. Hamming code detects and corrects the errors that can occur when the data is moved or stored from the sender to the receiver. This simple and effective method helps improve the reliability of communication systems and digital storage. It adds extra bits to the original data, allowing the system to detect and correct single-bit errors.

What are Redundant Bits?

Redundant bits are extra binary bits that are generated and added to the information-carrying bits of data transfer to ensure that no bits are lost during the data transfer. The number of redundant bits can be calculated using the following formula:

 2r ≥ m + r + 1 

where,

• m is the number of bits in input data

• r is the number of redundant bits.

Suppose the number of data bits is 7, then the number of redundant bits can be calculated as

= 24 ≥ 7 + 4 + 1 

Thus, the number of redundant bits is 4.

Types of Parity Bits

A parity bit is a bit appended to a data of binary bits to ensure that the total number of 1’s in the data is even or odd. Parity bits are used for error detection. There are two types of parity bits:

• Even Parity Bit: In the case of even parity, for a given set of bits, the number of 1’s are counted. If that count is odd, the parity bit value is set to 1, making the total count of occurrences of 1’s an even number. If the total number of 1’s in a given set of bits is already even, the parity bit's value is 0.

• Odd Parity Bit: In the case of odd parity, for a given set of bits, the number of 1’s are counted. If that count is even, the parity bit value is set to 1, making the total count of occurrences of 1’s an odd number. If the total number of 1’s in a given set of bits is already odd, the parity bit's value is 0.